Für die rotatorische Betrachtung von Antriebssträngen ist immer ein komplexeres Modell nötig, da hier immer ein Gesamtmodell aufgebaut werden muss.

Bei biegekritischen Eigenfrequenzen und Eigenformen können sinnvolle Teilsysteme abgegrenzt und aufgebaut werden, und davon dann ein Simulationsmodell aufgebaut werden. Beispielweise an einer Gelenkwelle kann unter Berücksichtigung der Masse des einen Gelenkkopfes und der halben Masse der Zwischengelenkwelle eine solche Auftrennung gemacht werden. Die Eigenfrequenzen für Biegung sind dann hierbei recht präzise zu ermitteln ungeachtet dessen, wie es auf der anderen Seite der Gelenkwelle weitergeht.

Bei Drehschwingungsmodellen ist es deutlich schwieriger solche Trennstellen zu finden und dann Stück für Stück zu analysieren. Wenn man das machen würde, wäre die Gefahr dass tatsächliche Beeinflussung der Teilstränge zueinander zu falschen Eigenfrequenzaussagen führen viel zu groß. Deswegen sollte das Drehschwingungssystem immer komplett abgebildet werden.

Unterschiedliche Methoden zur Resonanzermittlung

1. •Einfache weil kurze Wellenstränge können direkt im CAD-Programm mittels FE-Simulation ermittelt werden. Bei Creo/ProE gibt es Pro/Mechanica, bei CATIA V5 gibt es das CATIA-FEM und bei Siemens NX gibt es Advanced Simulation. Alle diese Werkzeuge arbeiten nach dem gleichen Prinzip: es werden Bauteile fest miteinander verbunden (verschweisst) und über die Geometrie mitsamt der Werkstoffeigenschaften Dichte, E-Modul und Querkontraktionsmodul werden die Drehsteifigkeiten optimal und automatisch berechnet. Jetzt noch die richtigen Einspannbedingungen wie z.B. Lagerstellen angegegeben und am Schluss bekommt man neben ALLEN Resonanzfrequenzen (Biegung, Torsionen, Längsschwingen usw.) auch deren Biegemode als Animation angezeigt. Diese Werkzeuge sind sehr anschaulich und lassen eine gute ingeieurmäßige Analyse und Basis für Optimierungen zu.
   
   Aber ihr Nachteil liegt darin, dass alle Bauteile wie eine feste Masse miteinander verbunden sein müssen. Kopplungen wie Gelenke zwischen 2 Bauteilen sind derzeit nicht möglich.
   
   

2. •Es gibt wiederum Mehrkörper-Module in den obigen CAD-Werkzeugen die eine komplexe Kopplung zwischen Bauteilen untereinander zulassen ... aber dann wird z.B. eine Welle als starr betrachet und hat keine Eigenfrequenz aufgrund ihrer Struktur und Eigenverformung. Diese CAD-Module heißen z.B. Pro/Kinematik bei Creo/ProE, SimDesigner bei CATIA V5 oder NX motion bei Siemens NX.
   
   Mit diesen Systemen lassen sich in sich starre Massen die bereits im CAD vorliegen recht schnell und einfach in allen 3 Raumrichtungen miteinander koppeln und verbinden. Auch ungleichmäßige übertragende Getriebe können hier recht gut simuliert werden. Hinsichtlich unserer Aufgabe der Ermittlung der Drehschwingungs-Eigenfrequenzen können diese Systeme eine sehr gute Hilfe sein und gute Ergebnisse liefern. Der große Vorteil ist die anschließende Darstellung des Schwingsystems als Film in 3D.
   
   Der große Nachteil ist, dass Bauteile wie Wellen in sich aufgetrennt werden müssen und in Teilsysteme bestehend aus Massenträgheiten und Drehfedern aufgetrennt werden müßten, um wirklich alle Resonanzfrequenzen zu erwischen. Dabei würde viel Aufwand in die CAD-technische Auftrennung der Wellen in Teilsysteme entstehen.
   
   

3. •Mit Werkzeugen wie Simulink Simscape lassen sich Drehsysteme aus zahlreichen Grundelementen wie Massenträgheiten, Drehfedern, Getrieben, Bremsen, Kupplungen usw. aufbauen. In jedem Grundelement können mehr oder weniger tief Werte des jeweiligen Bauteilverhalten hinterlegt werden wie beispielsweise die Wirkungsgrade und Verluste in Getrieben.
   
   Um eine Welle in einem solchen System korrekt zu modellieren sollte diese auf größere Masseansammlungen untersucht und zwischen diesen aufegtrennt werden. Die Welle besteht dann aus Massenträgheiten und Drehfedern die diese miteinander verbinden. Die Massenträgheiten der Einzelmassen sollten realistisch sein genauso wie die Drehfeder-Steifigkeiten. Da hierbei die gesamten Systeme auf ein reines Drehschwingungssystem reduziert wird und alle radialen Biegeschwingungen unter den Tisch fallen spricht man von diesen Modellen von 1D-Modellen.
   
   Der Nachteil dieser Werkzeuge ist es, dass die Massenträgheiten und die Federsteifigkeiten immer erst ermittelt werden müssen. Einfache Wellen können zwar mit analytischen Methoden bestimmt werden, aber dabei können viele Fehler durch Vereinfachungen gemacht werden, die das Ergebnis wiederum verfälschen können.
   

Zusammenfassend kann folgendes sagen: warum immer nur ein System alleine verwenden. Wenn es bestimmte Vorteile hat die Eigenfrequenzen einer elastischen Welle die es bereits im CAD sehr detailliert modelliert gibt, dann sollte das CAD-basierte System verwendet werden. Durch die Anzeige der Eigenmoden bekommt man sehr anschaulich das Schwingungssystem dargestellt und kommt vielleicht auf Moden, an die man bislang gar nicht gedacht hat.

Bei komplexen Wellensträngen kommt man nicht umhin ein 1D-Modell aufzubauen. Hier können aber zur Modellvereinfachung auf die Zerlegung der Wellen in Teilssysteme verzichtet werden, wenn die Eigenfrequenzen der elastischen, zusammenhängenden Bauteile im CAD-basierten System ermittelt werden.

Dann ergibt sich der wahre Vorteil: durch die Auftrennung der Aufgabe in elastische Frequenzermittlung über CAD-gestützte Berechnungswerkzeuge und Feder-Masse-Systeme mittels Simulink Simscape können sehr schnell gute Ergebnisse ermittelt werden.

Wenn es um die Schwingamplitudenermittlung geht, kommen wir um ein komplexes Modell in nur einem System nicht herum. Hier ist Simulink SimScape die erste Wahl, auch weil es vielleicht in einem freühen Entwicklungsstadium noch nicht alle Bauteile im 3D-Programm gibt.

Beispiel eines 3-Massenschwingers

Wir haben hier mit einem einfachen Schwingungssystem eine Gegenüberstellung der Systeme gemacht. Es handelt sich um ein 3-Massensystem gekoppelt über Drehfedern. Wir verwenden eine CAD-gestützte Methode in Siemens NX Motion und 2 Methoden in Matlab Simulink Simscape.

Verfahren 1 - NX-nastran-Modell mit FE-Modalanalyse

Als Ergebnis einer Modalanalyse aus dem FE-Programm erhält man eine Darstellung als Filmanimation der Schwingbewegung. Durch das Netz und die Einfärbung der großen Auslenkungen (rot) im Verhältnis zu keinen Auslenkungen (blau) erhält man einen guten Eindruck des Schwingungsphänomen.

Verfahren 2 - SimScape-Modell mit Auslenkung der Federn ohne externe Anregung

Bei diesem Verfahren wird das 1D-Systemmodell aufgebaut.

Alle Federn werden zum Zeitpunkt t=0 Sekunden auf einige Grad ausgelenkt. Somit befindet sich Energie in den Federn und das System beginnt mit seinen verschiedenen Eigenmoden zu schwingen.

Die Schwingungen werden über Drehwinkelgeber (Basiselement „Ideal Rotational Motion Sensor“) bezüglich dem Welt-Koordinatensystem aufgezeichnet und dann kann man darauf die jeweiligen Schwingwege der einzelnen Drehmassen analysieren.

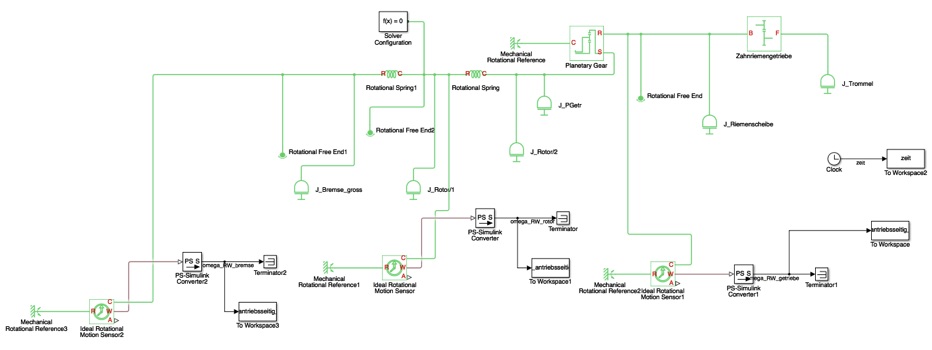
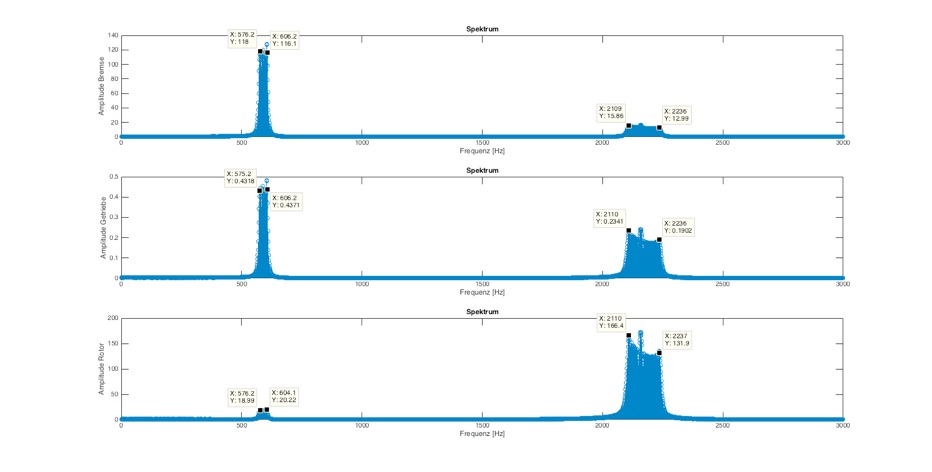
Verfahren 3 - SimScape-Modell mit Anregung über Sinus-Sweep

Bei diesem Verfahren wird zu 95% dasselbe Modell wie bei Verfahren 2 verwendet. Dabei werden die dort eingetragenen Auslenkungen der Federn auf Null gesetzt bzw. herausgenommen. Ergänzt wird das Modell um ein Chirp-Element mit entsprechender Aktor wie einer idealen Drehmomentenquelle oder einer idealen Drehwinkelgeschwindigkeitsquelle.

Wenn ein komplexes Modell verwendet wird und an einem Ende des Modells der Sinus-Sweep aufgebracht wird und Dämpfer im Einsatz sind kann es sein, dass bestimmte Drehmoden durch die Dämpfung am anderen Ende gar nicht mehr angeregt werden. Das bedeutet dann nicht dass es diese nicht gibt, sondern dann muss das Sinus-Sweep auch mal versetzt werden und an mehreren Stellen nacheinander angeregt werden. Die Amplitude ist dann sehr unterschiedlich, aber solange die Schwingsysteme in Resonanz kommen macht das nichts aus ... denn wir sind ja lediglich an den Frequenzen und nicht an der Amplitude interessiert (im ersten Schritt).

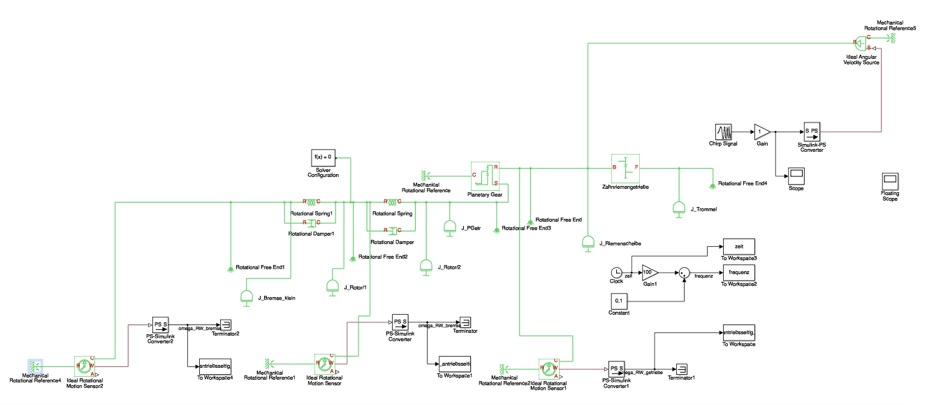
Probleme bei der Frequenzanalyse mit Matlab

1. •Es muss ein Solver mit fester „Step-size“ aufgewählt werden. Ansonsten ist der Zeit und der Frequenzstrahl nicht linear und bei der fft wird eine willkürliche Abtastfrequenz ermittelt, die nicht für die gesamte Messung gültig ist. Dadurch kommt es zu Fehlinterpretationen der fft-Funktion. Man sieht dies auch auf der Darstellung des RPM-Zeit-Diagramm bei der rpmfreqmap-Funktion (Frequency Map)
   

2. •Die Step-Size sollte so gewählt werden, dass gilt: Abtastfrequenz >= 2x zu untersuchende Frequenz …. Also bei 3000 Hz ergibt sich 1/6000Hz = 0,000167s (Step-Size)
   

Step-Size

1. •Delta_T=0,001 (schlecht): es können keine höheren Frequenzen ermittelt werden, alle Frequenzen sind ziemlich gleichverteilt im niederfrequenten Bereich
   

2. •Delta_T=0,0001 (mässig gut): Frequenzanalyse zeigt die Resonanzen mäßig gut an … alles wirkt aber noch verschwommen. Aber es werden erkannte Frequenzen vom gesamten Frequenzbereich angezeigt.
   

3. •Delta_T=0,00001: die Berechnung dauert sehr lange (5min). Eventuell kann mit um eine Zehner-Potenz reduzierten Step-Size und erhöhten Dämpfungswerten ein besseres und schnelleres Ergebnis ermittelt werden.
   

4. •Ein weiterer Parameter ist die Dämpfung der Federn mit parallel geschaltetem Dämpfer (Dämpfungswerte von 0,01 über 0,5 bis 1 Nm/(rad/s). Damit das Schwingsystem auch den hochlaufenden Anregungsfrequenzen anpassen kann und sich die einmal hineingesteckte Energie wieder abbauen kann, ist die Dämpfung wichtig. Eine zu niedrig gewählte Dämpfung schlägt sich in einem Verwaschen der Resonanzfrequenzen nieder.
   

Parameter-Studie zur optimalen Wahl der Simulations-Parameter

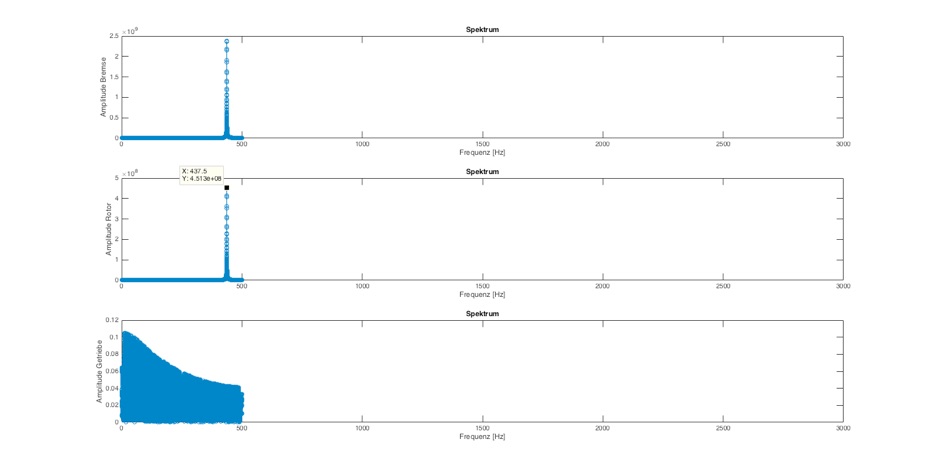
Abb.: Frequenzanalyse mit delta_T=0,001 und Dämpfung=0 Nm/(rad/s) bei 3000 Hz

Hier kann man erkennen, dass die ermittelten Frequenzen nicht das komplette Anreungsspektrum bis 3000 Hz anzeigen, sondern nur bis 500 Hz. In diesem Fall ist die Abtastung zu grob, so dass die Sinus-Kurven nicht sauber dargestellt werden und damit auch nicht die korrekten Oberfrequenzen erkannt werden können.

Bei Dämpfung 0 wird trotzdem bereits eine Resonanzfrequenz korrekt erkannt.

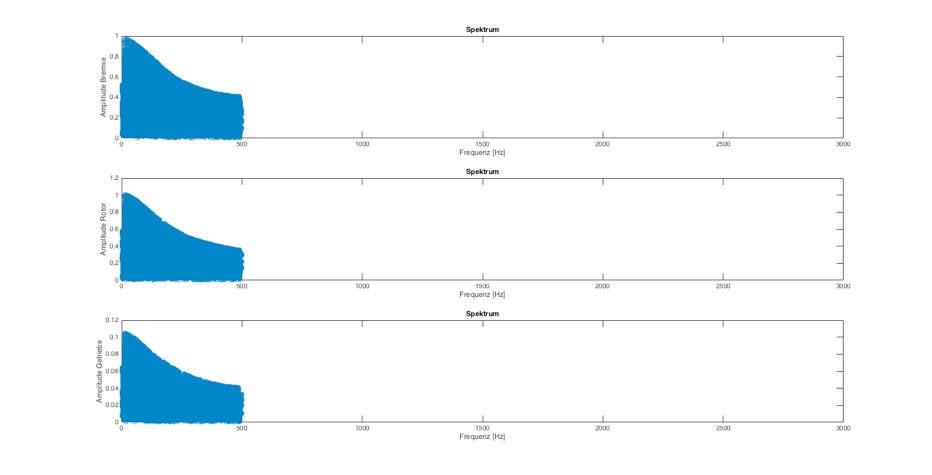
Abb.: Frequenzanalyse mit delta_T=0,001 und Dämpfung=0,5 Nm/(rad/s) bei 3000 Hz

Hier kommt zu einer zu geringen Abtastrate noch eine zu hohe Dämpfung, wodurch keine Resonanz mehr gefunden werden kann.

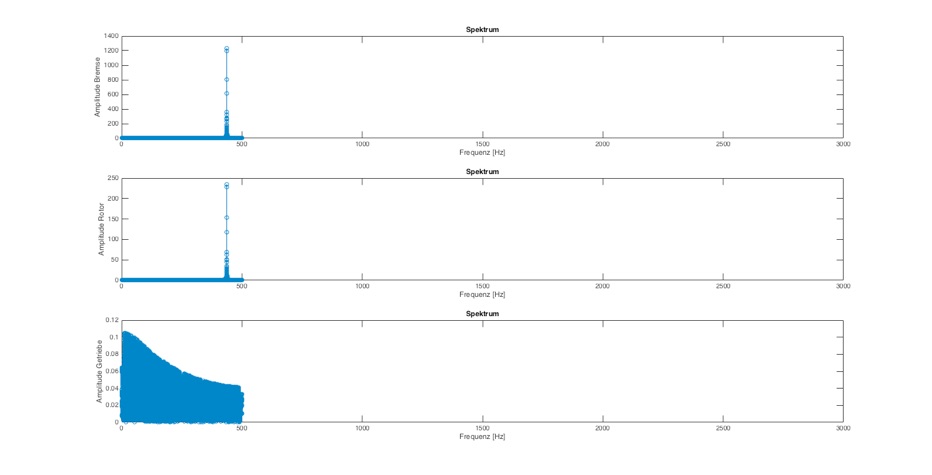
Abb.: Frequenzanalyse mit delta_T=0,001 und Dämpfung=0,0001 Nm/(rad/s) bei 3000 Hz

Hier ist die Dämpfung bereits optimal, aber die Abtastrate zu schlecht.

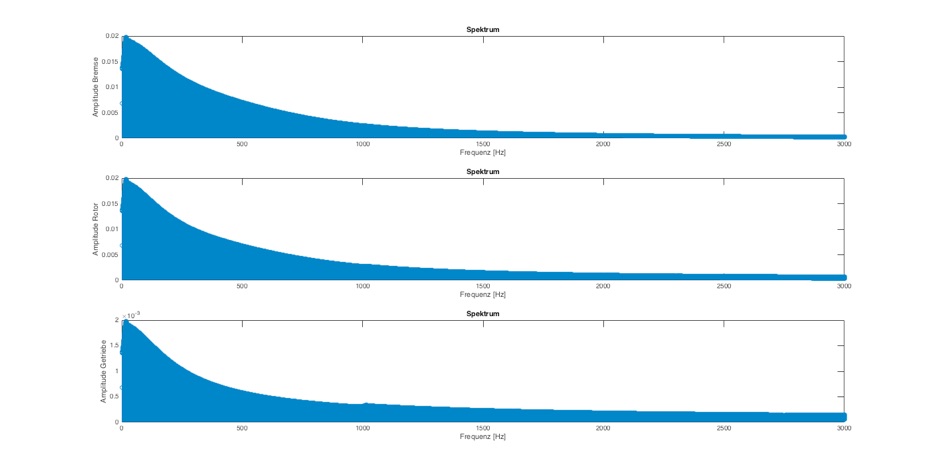
Abb.: Frequenzanalyse mit delta_T=0,0001 und Dämpfung=0,5 Nm/(rad/s) bei 3000 Hz

Hier stimmt die Abtastrate. Das kann man daran sehen dass das gesamte angeregte Frequenzspektrum auch erkannt wird, allerdings noch ohne die REsonanzfrequenzen aufgrund der zu hohen Dämpfung.

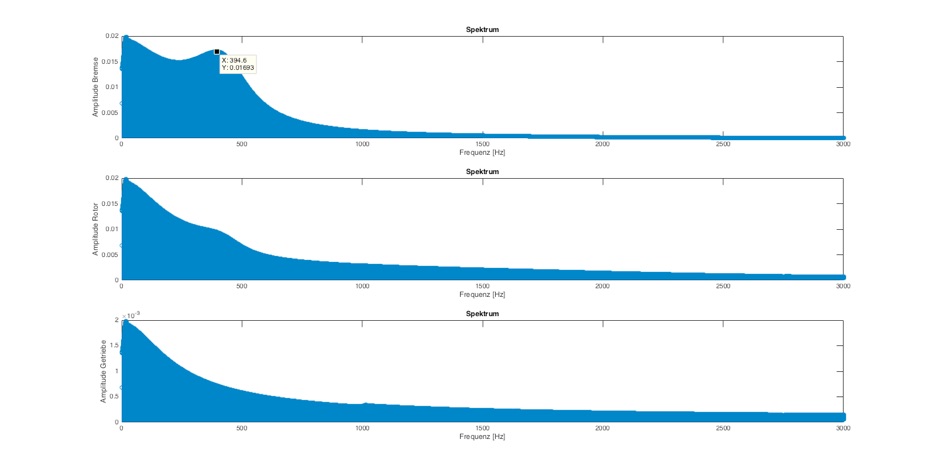
Abb.: Frequenzanalyse mit delta_T=0,0001 und Dämpfung=0,1 Nm/(rad/s) bei 3000 Hz

Nimmt man die Dämpfung sukzessive zurück, so werden sehr langsam die ersten Resonanzen sichtbar. hier erst man die 1. Eigenfrequenz.

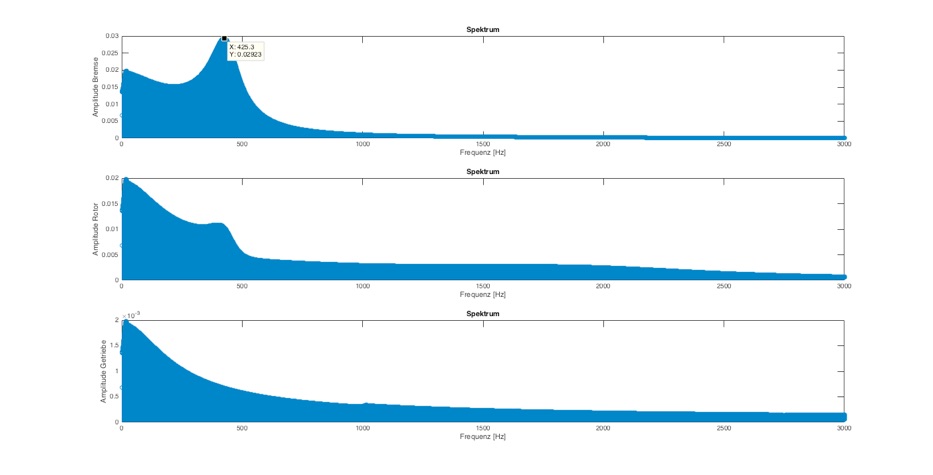
Abb.: Frequenzanalyse mit delta_T=0,0001 und Dämpfung=0,05 Nm/(rad/s) bei 3000 Hz

Nimmt man die Dämpfung weiter zurück kommt auch langsam die zweite Resonanzfrequenz zum Vorschein.

Abb.: Frequenzanalyse mit delta_T=0,0001 und Dämpfung=0,01 Nm/(rad/s) bei 3000 Hz

Die Resonanzen werden immer klarer sichtbar und immer schmalbandiger dargestellt.

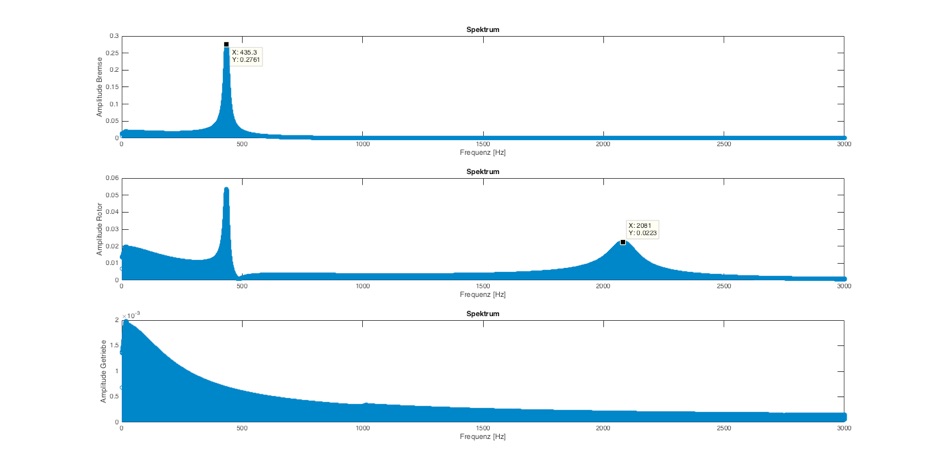
Abb.: Frequenzanalyse mit delta_T=0,0001 und Dämpfung=0,005 Nm/(rad/s) bei 3000 Hz

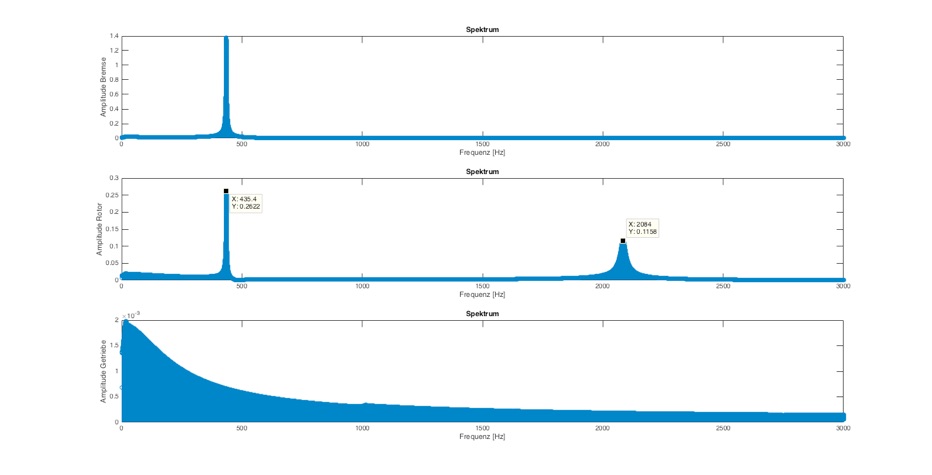
Abb.: Frequenzanalyse mit delta_T=0,0001 und Dämpfung=0,001 Nm/(rad/s) bei 3000 Hz

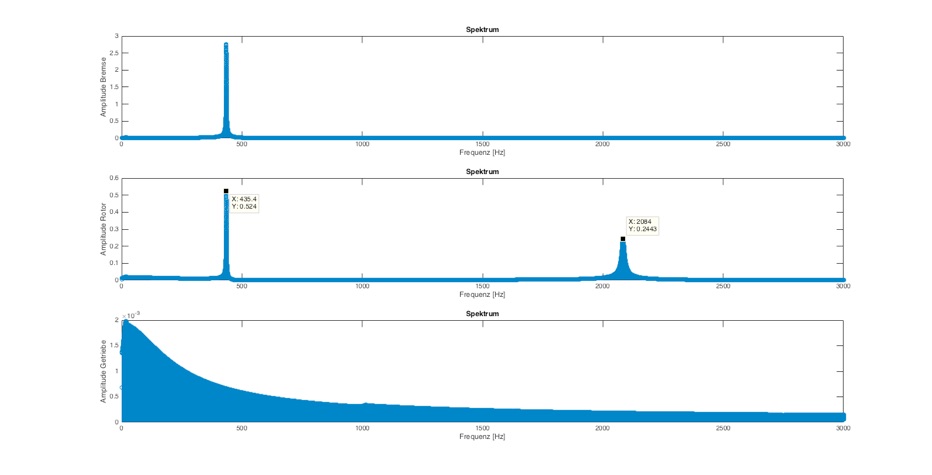
Abb.: Frequenzanalyse mit delta_T=0,0001 und Dämpfung=0,0005 Nm/(rad/s) bei 3000 Hz

Diese Auswertung zeigt bereits beide Resonanzfrequenzen, wobei die höhere Frequenz etwas breitbandiger angeregt wird.

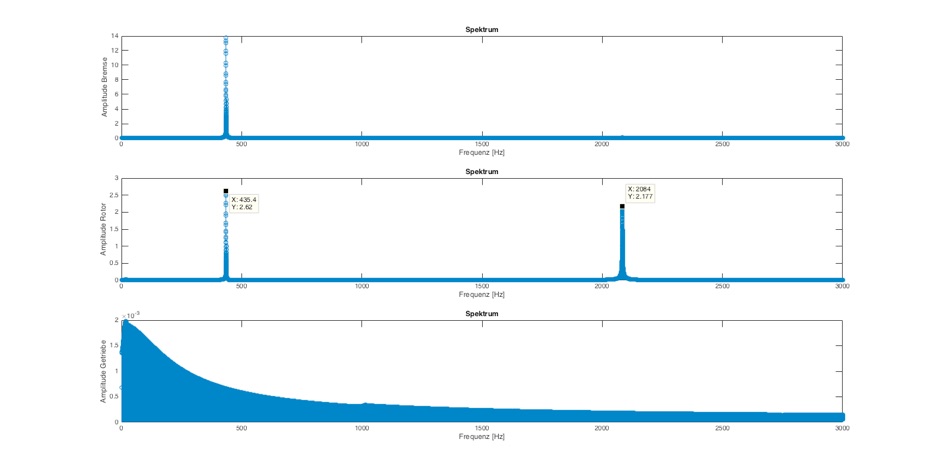
Abb.: Frequenzanalyse mit delta_T=0,0001 und Dämpfung=0,0001 Nm/(rad/s) bei 3000 Hz

Diese Auswertung zeigt sehr schön beide Resonanzfrequenzen an. Man merkt dass der Sinus-Sweep an der Getriebeseite angreift und diese daher fremdgesteuert ist und gar nicht erst in Resonanz kommen kann. Also sollte man sich Gedanken machen, wo die Anregung eingeleitet wird.

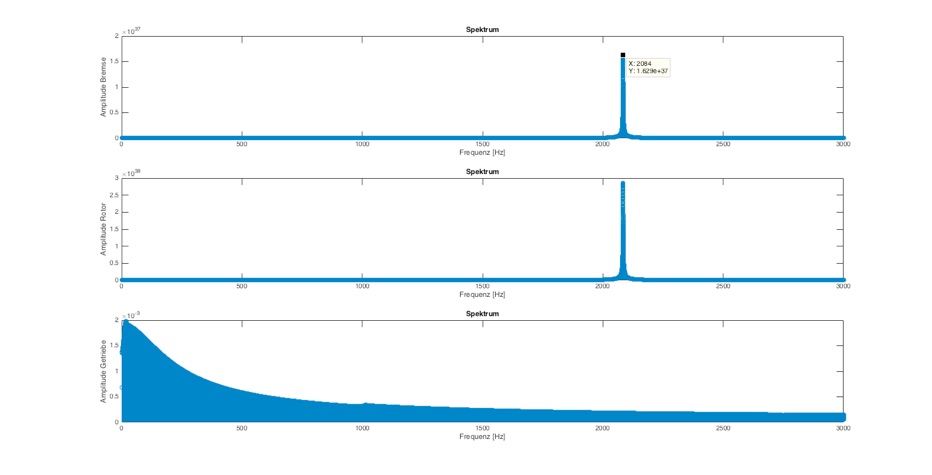
Abb.: Frequenzanalyse mit delta_T=0,0001 und Dämpfung=0 Nm/(rad/s) bei 3000 Hz

Komplett ohne Dämpfung wird die erste Eigenfrequenz nicht erkannt, zudem ist die Amplitude der 2. Eigenfrequenz exorbitant hoch, so dass keine Energie mehr für die Anregung der anderen Resonanzen übrig bleibt.

Fazit:

1. •Die Step-Size sollte abhängig von der zu untersuchenden max. Frequenz bestimmt werden (siehe Beispielrechnung oben). Eine höhere Step-Size bringt keinen Mehrwert, bedeutet aber mehrere Minuten Berechnungszeit. Die Step-Size ist hoch genug, wenn bei der fft-Analyse im gesamten Frequenzband Punkte angezeigt werden.
   

2. •Eine angemessene Dämpfung erhöht die Trennschärfe der Resonanzfrequenzen, da beim Hochlauf Energien wieder abgebaut werden und damit sich das Feder-Masse-System ausreichend schnell auf die neuen Anregungsfrequenzen anpassen kann. Die Dämpfung sollte bei mehreren Simulationsläufen verändert werden um sicherzustellen, dass alle Resonanzfrequenzen erkannt werden. Ein guter Startwert ist dabei eine Dämpfung von 0,0001 bis 0,0005 Nm/(rad/s). Treten nach mehrmaliger Variation der Dämpfung keine neuen Resonanzen mehr auf und liegen ihre Pegel auf nahezu gleicher Amplitudenhöhe so kann davon ausgegangen werden dass man alle Resonanzen erwischt hat. Für jede Feder in einem Masse-Feder-System muss es eine Resonanz geben.