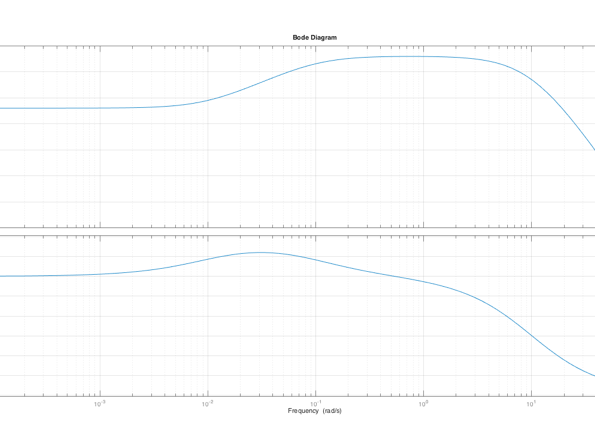
Mit dem Matlab-Befehl bode() kann ein BODE-Plot einer Übertragungsfunktion erzeugt werden.

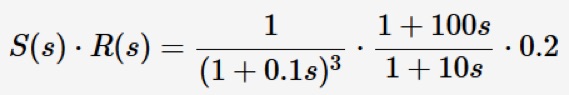
Der Zähler ergibt sich ausmultipliziert: 20s +0.2

Der Nenner ergibt sich ausmultipliziert: 0.01s4 + 0.301s3 + 3.03s2 + 10.3s +1

•H1=tf([20 0.2],[0.01 0.301 3.03 10.3 1]);

•bode(H1)

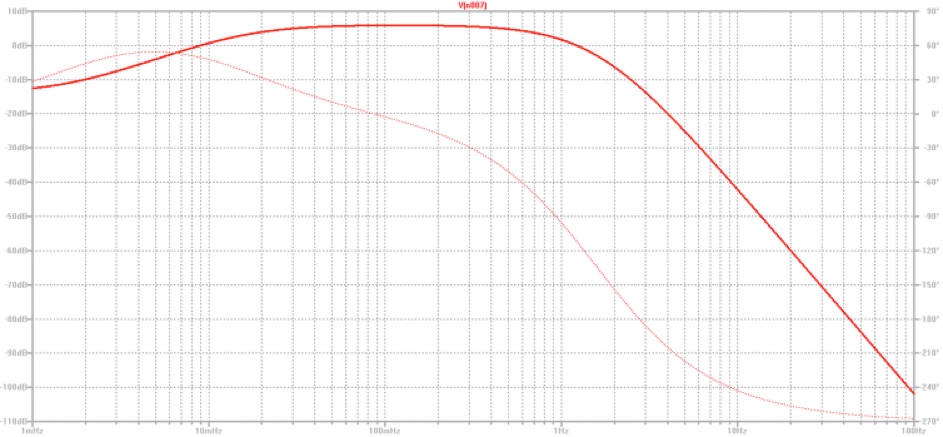
Wie wird das "Stabilitätskriterium aus dem Bode Diagramm" (Phasenreserve) allgemeingültig und präzise formuliert?

Man lernt ja nun für ein stabiles System, dass bei der Frequenz, wo A=0dB ist die Phase noch größer als -180° sein muss. Was heißt das nun genau? Wenn ich z.B. eine Phase von -120° habe, ist das System stabil. Wäre die Phase -240°, so hätte man ein instabiles System.

Nun kann ich ja aber immer mod(360°) rechnen, also -240° entspricht 120°. Wenn ich das Kriterium wortwörtlich nehme, so ist 120° > -180° --> also stabil...

Ich kann ja den Winkel immer entweder negativ oder positiv zählen, was zählt nun?

Beispiel (offene Schleife):

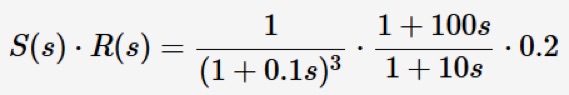
hat bei den Frequenzen wo der Betrag = 0dB ist Phasen von

1) bei f1=9mHz: +50°

2) bei f2=1.23Hz: -112°

Das geschlossene System ist definitiv stabil (siehe Abbildung oben).

phi = arctan(100*w) -3*arctan(0,1*w) -arctan(10*w)

Jetzt einfach bei 0dB schauen wie weit man noch von -180° entfernt ist. Das ist die Phasenreserve. Das ist hier bei 1.1Hz und phi=-100°. Daraus folgt die Phasenreserve beträgt 80°. Damit wird auch das rückgekoppelte System stabil sein.

Man darf das BODE-Diagramm für Stabilitätsbetrachtungen nicht „bedenkenlos“ anwenden.

Das heißt: Es gibt Funktionen für die Schleifenverstärkung L(s), bei denen die „vereinfachte Form“ des Stabilitätskriteriums nicht angewendet werden darf.

Andererseits ist das BODE-Diagram ja weiter nichts als die getrennte Darstellung von Betrag und Phase aus dem Nyquist-Diagramm - beihaltet also exakt die gleichen Informationen. Und damit liefert es auch die gleichen Stabilitätsinformationen wie das Nyquist-Diagram. Es kommt nur darauf an, das Kriterium in der richtigen Form auf das BODE-Diagramm zu übertragen.

Und im vorliegenden Fall darf das "vereinfachte" Kriterium nicht angewendet werden, da die 0dB-Linie von der Betragsfunktion zweimal geschnitten wird. Vielmehr muss das Kriterium in seiner allgemeinen Form angewendet werden, welches - auf das BODE-Diagrammm übertragen - für den vorliegenden Fall lautet:

"Der geschlossene Kreis ist dann stabil, wenn im BODE-Diagramm für die Funktion L(jw)(Produkt der Übertragungsfunktionen der Kette) die im Bereich |L(jw)| > 0dB auftretenden Übergänge des PHASENGANGS durch die 180-Grad-Linie folgende Bedingung erfüllen:  S(+) = S(-).Dabei ist S(+) die Zahl der Phasenübergänge mit positiver und S(-) mit negativer Steigung.
Voraussetzung: L(s) hat keine Pole mit positivem Realteil, was ja zumeist erfüllt ist (offenen Kette stabil).

Im vorliegenden Fall ist S(+)=S(-)=0 und das Stabilitätskriterium also erfüllt.

Zur Verdeutlichuing: Stellt man sich ein kompliziertes System vor, bei dem L(s) die negativ-reelle Achse links vom kritischen Punkt schneidet (Phase -180, Betrag>1), dann verlangt das Kriterium einen zweiten Schnittpunkt mit der Achse in der anderen Richtung (Rückkehr in den 3. Quadranten), damit der Punkt “-1“ nicht umschlossen wird. Also S(+)=S(-)=1. Klingt doch logisch, oder?Ich hoffe, dass Dir das ein wenig weiter hilft. Wenn ich das noch sagen darf: Ich begrüße Deinen Wunsch nach Exaktheit auch in der Ausdrucksweise - das ist eine ganz wichtige Voraussetzung, um Missverständnisse zu vermeiden.

Noch einmal zusammengefasst:

(1)Das "vereinfachte" Stabilitätskriterium im BODE-Diagramm (definiert über Phasen- bzw. Verstärkungsreserve) darf angewendet werden unter den folgenden drei Voraussetzungen:

•Die Übertragungsfunktion der offenen Kette L(s) ist stabil (keine Pole in der rechten Halbebene);

•Die Betragsfunktion schneidet die 0-dB-Linie nur einmal;

•Die Phasenfunktion schneidet die 180-Grad-Linie nur einmal.

Eine weitere Vereinfachung (ohne Kenntnis des Phasengangs) ist erlaubt, sofern die Funktion L(s) ein Mindestphasen-System darstellt (keine Allpass-Elemente enthält). In diesem Fall ist die Stabilität des geschlossenen Systems gegeben, wenn die Abnahme der Betragsfunktion |L(jw)| beim Durchgang durch die 0-dB-Linie zahlenmäßig geringer ist als 40dB/Dekade.

(2)Andernfalls ist das allgemeine Stabilitätskriterium nach Nyquist (bzw. die Adaption für das BODE-Diagramm) anzuwenden.