Mit der Allzweck-Waffe Matlab lassen sich vielfälitge Aufgaben und Problemstellungen angehen und lösen. Dabei gibt es verschiedene Funktionen, welche immer wieder verwendet werden und diese am häufigsten einsetzbaren Funktionen und vor allem ihre Anwendung möchte ich hier aufzeigen.

Wenn aus gemessenen Wartepaare (x- und y-Wertereihen) eine Näherungsfunktion ermittelt werden soll, so gibt es die Funktion polyfit()

p = polyfit(x,y,n)

Dabei ist n den Polynomgrad der Näherungsfunktion, x und y sind die Wertetabellen. Der Näherungsalgorythmus funktioniert nach dem Verfahren der minimalen quadratischen Abweichung (Regression).

Im Prinzip ist die Funktion ganz einfach. Es gibt beispielsweise gemessen Werte, welche aus x-y-Koordinaten bestehen ... beispielsweise eine Kennlinie eines Sensorsystems. Würde man beispielsweise einen neuen X-Wert als gegeben haben und möchte den zugehörigen Funktionswert y, dann müsste man ohne Näherungsfunktion bildlich gesehen in die Wertetabellen gehen und den am nächsten liegenden Wert herauslesen. Das geht zwar ist aber ungenau und mit Programmieraufwand verbunden ... do hat man es früher gemacht.

Ganz einfach wird es, wenn man die Wertetabellen in eine Funktion n-ten Grades überführt. Man muss sich jetzt nur noch die Koeffizienten merken und vielleicht noch die alten Grenzen der Messwerte, die Wertereihen kann man löschen.

Noch ein Wort zu Näherungsverfahren generell. Deren Güte kann ermittelt werden und damit der Abweichungsfehler beliebig klein gehalten werden ... einfach indem man den Polynomgrad erhöht. Außerhalb der gegebenen Wertepaare wird die Abweichung stark anwachsen, weil ja nicht bekannt ist wie dort die Kennlinie aussieht. Trotzdem würde die Funktion dort einen Wert ausspucken. Es ist also eine Grenzwertüberprüfung notwendig, damit nur interpolierte und keine extrapolierte Werte verwendet werden.

Als Ergebnis enthält p die Koeffizienten der Näherungsfunktion.

Um einen Polynom beliebigen Grades anzulegen, werden die Koeffizienten in eine Liste geschrieben, also beispielsweise für

y= 2x3 + 4x2 + 5x +10

>> p = [2 4 5 10]

p =

     2     4     5    10

y = polyval(p,x)

Um einen bestimmten x-Wert in diesen Polynom einzusetzen und das Ergebnis errechnen zu lassen steht die Funktion polyval() zur Verfügung. p ist die Reihen mit den Koeffizienten einer Polynom-Näherungsfunktion, x ist der Wert zu dem der Funktionswert ermittelt werden soll.

Beispiel: X=20

>> polyval(p, 20)

ans =

       17710

Es können auch mehrere X-Werte ausgewertet werden mit

>> polyval(p, [3 8 7])

ans =

         115        1330         927

syms x y

Mit der symbolischen Bibliothek kann man auch direkt Gleichungen eingeben. Zuerst sollen die Variablen gekennzeichnet werden über syms. Damit wird gekennzeichnet, dass x und y eine Variable im Sinne der symbolischen Bibliothek ist.

>> syms x

>> g = p(1)*x^3 + p(2)*x^2 + p(3)*x + p(4)

g =

2*x^3 + 4*x^2 + 5*x + 10

S = solve(eqn,var)

Mit diesem Gleichungslöser kann man Polynome eqn nach einer beliebigen Variablen var auflösen lassen. Hier ein Beispiel

syms a b c x

sol = solve(a*x^2 + b*x + c == 0)

sola = solve(a*x^2 + b*x + c == 0, a)

sol =

-(b + (b^2 - 4*a*c)^(1/2))/(2*a)

-(b - (b^2 - 4*a*c)^(1/2))/(2*a)

sola =

-(c + b*x)/x^2

Hier ein Beispiel, wie 2 Polynome gleichgesetzt und anschließend nach Variablen aufgelöst werden können.

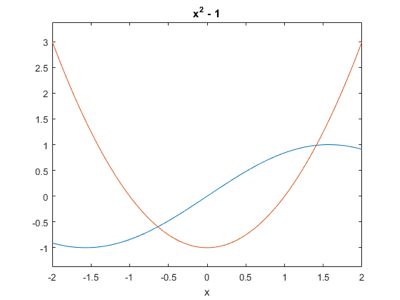
ezplot(sin(x), -2, 2)

hold on

ezplot(x^2 - 1, -2, 2)

hold off

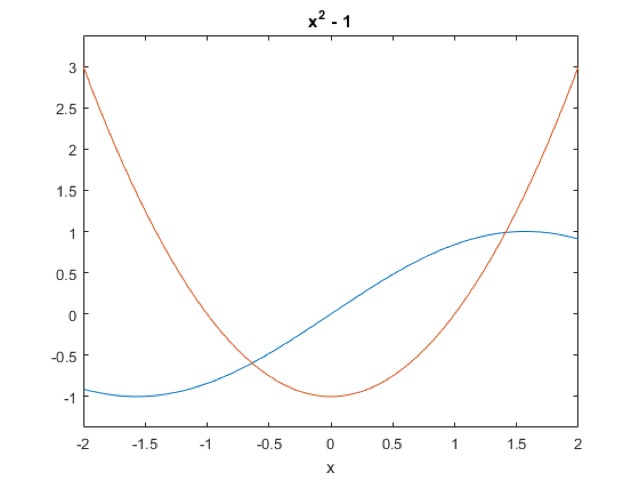
vpasolve(sin(x) == x^2 - 1, x, [0 2])

ans =

1.4096240040025962492355939705895

Es lassen sich Ergebnisse als Funktion darstellen oder auch als Zahlenwert.

syms x

solve(x^5 == 3125, x)

ans =

                                                          5

- (2^(1/2)*(5 - 5^(1/2))^(1/2)*5i)/4 - (5*5^(1/2))/4 - 5/4

   (2^(1/2)*(5 - 5^(1/2))^(1/2)*5i)/4 - (5*5^(1/2))/4 - 5/4

   (5*5^(1/2))/4 - (2^(1/2)*(5^(1/2) + 5)^(1/2)*5i)/4 - 5/4

   (5*5^(1/2))/4 + (2^(1/2)*(5^(1/2) + 5)^(1/2)*5i)/4 - 5/4

solve(x^5 == 3125, x, 'Real', true)

ans =

5