Im dritten Teil möchten wir uns das 4-Gang-Planetengetriebe genauer ansehen. Dieses wird aus mehreren Blocken zusammengebaut.

Ein Planetengetriebe besteht aus verschiedenen Planetensätzen, die hintereinander bzw. gekoppelt angeordnet sind. Weiterhin gibt es Bandbremsen, die Drehfreiheitsgrade schaltbar unterbinden können oder zulassen. Schaltbare Kupplungen dienen dazu 2 drehende Teile miteinander zu verbinden.

Weiterhin brauchen wir eine Steuereinheit welche die Gänge schalten kann. Vereinfacht kann auch ein Gang fest eingestellt und während der Simulation nicht verändert werden.

Das hier verwendete Planetengetriebe verfügt über 4 Vorwärtsgänge und einen Rückwärtsgang. Es hat einen gekoppelten Ravigneaux-Radsatz und einen einfachen, nachgeschalteten einfachen Planetensatz.

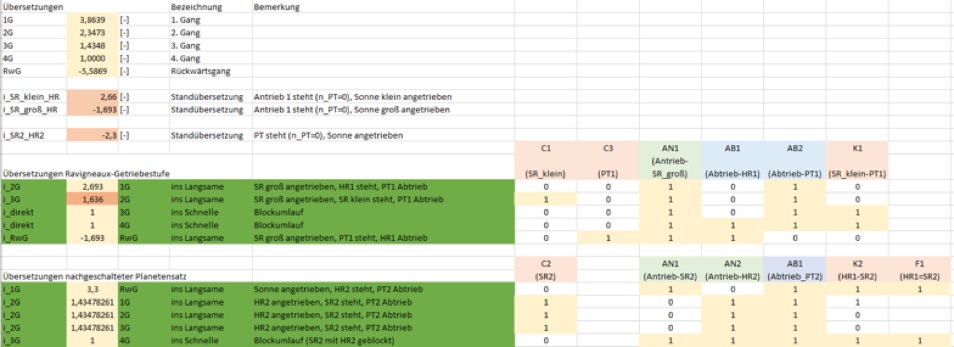
Für die beiden gekoppelten Planetensätze nach Ravigneaux gibt es einen eigenen gleichnamigen Block „Ravigneaux Gear“. Diesem können die beiden Standübersetzungen angegeben werden:

•iSR,klein-HR = 2,66

•iSR,groß-HR = 1,693

Für die nachgeschaltete einfache Planetenstufe PS2 gibt es den „Planetary Gear“-Block. Diesem kann die Standübersetzung angegeben werden

•iSR-HR2=2,3

Die Verschaltung des Ravigneaux-Radsatzes mit dem einfachen Planetensatz zu einem 4-Gang-Planetengetriebe erfolgt derart:

•wahlweise Kopplung von Planetenträger 1 mit Hohlrad 2 (Kupplung K1 offen, Bremse C3 offen)

•oder im Blockumlauf drehenden Radsatz 1 mit dem Hohlrad 2 (Kupplung K1 geschlossen, Bremse C3 offen)

•oder festgebremstes Hohlrad 2 zum Gehäuse (Kupplung K1 offen, Bremse C3 geschlossen)

Um die 4 Vorwärts- und den einen Rückwärtsgang zu schalten benötigt das Getriebe 2 Kupplungen und 3 Bremsen. Diese werden jeweils über „Disk Friction Clutch“-Blöcke realisiert, welche einen Schaltdruck als Eingang benötigen und dann ein entsprechend den im Block hinterlegten geometrischen Eigenschaften ein Reibmoment zwischen 2 Wellen aufbauen. Im vereinfachten Modell wird die Kupplung digital angesteuert, das heißt es liegt ein Druck von 0,9 MPa (90e5 Pa) bzw. 9 bar an und wird dann auf die Kupplungen bzw. Bremsen über das „PS Constant“-Element geleitet.

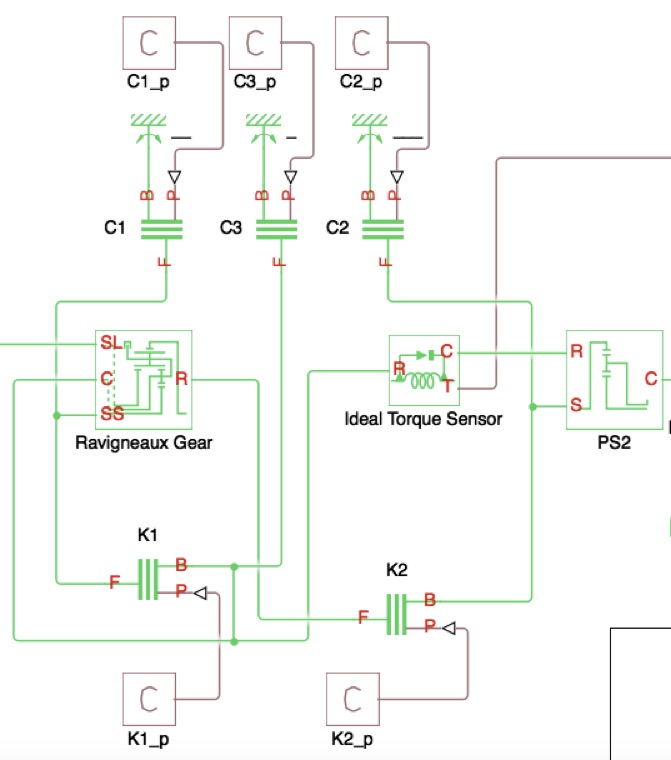
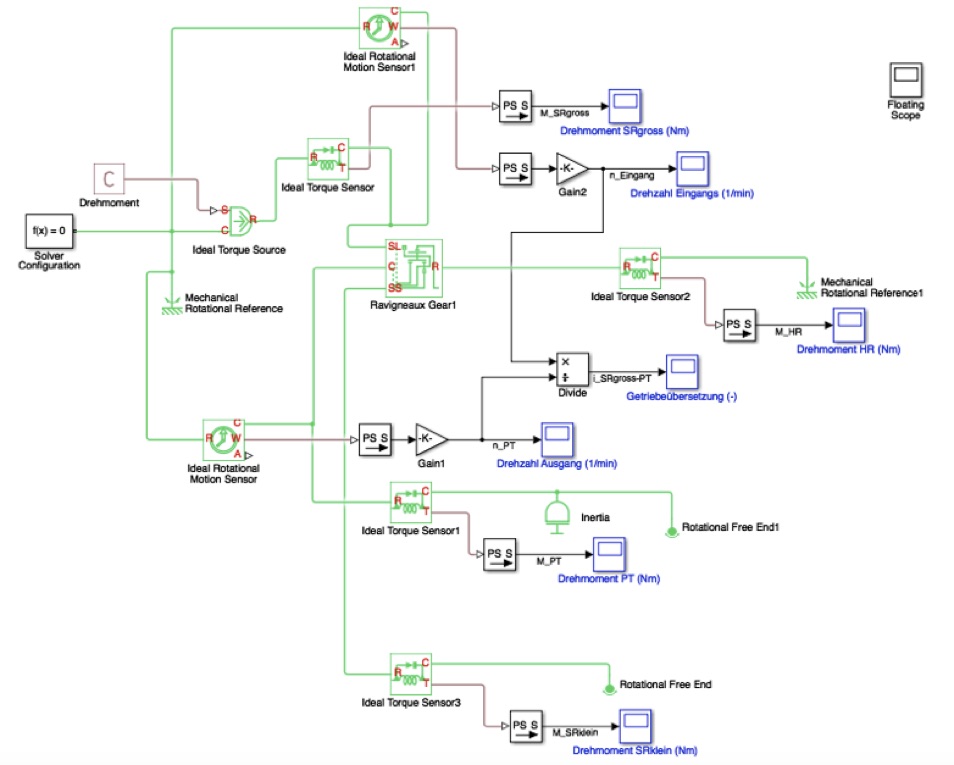
Wir möchten vereinfacht den ersten Gang fest eingelegt lassen und den Anfahrvorgang simulieren. Dazu wird in die „PS Constant“-Blöcke entweder 0 bar oder 9 bar eingetragen.

Für jeden Gang werden die Kupplungen und Bremsen verschieden angesteuert. Dabei kommen verschiedene Lastpfade zum Einsatz, für die die jeweiligen Komponentenbelastungen berechnet werden müssen.

Anbei die Lastpfade für die einzelnen Gänge:

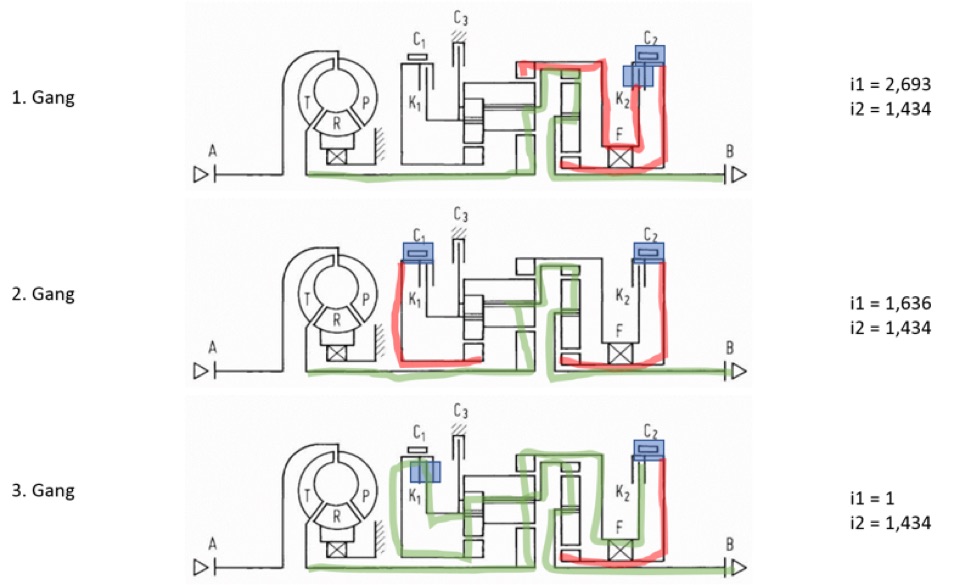
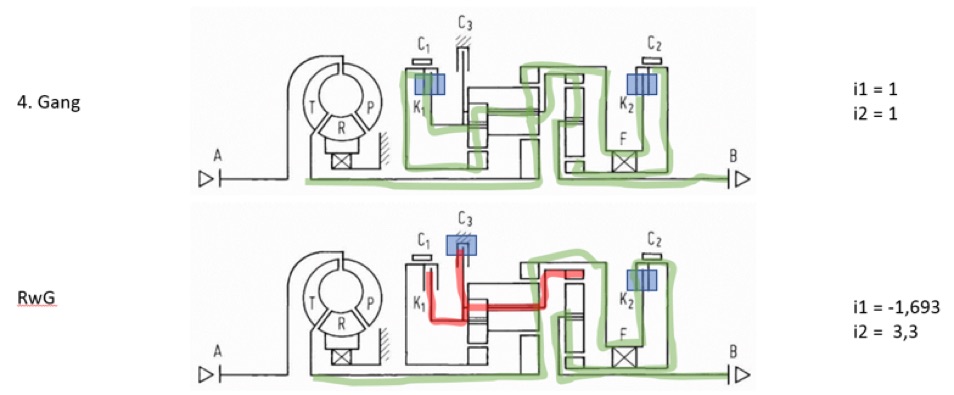
Betrachtung nur der Ravigneaux-Planetenstufe

Wenn wir uns die Ravigneaux-Stufe einzeln als Modell aufbauen dabei den ersten Gang geschaltet haben, so ergeben sich folgende Drehzahlen und Drehmomente:

•Eingang an SRgross – großes Sonnenrad  MSRgross = 200 Nm

•HR1 ist festgebremst  nHR1 = 0 1/min

•Abtrieb SRklein ist freidrehend  MSRklein = 0 Nm

•Momentenbelastung am Hohlrad (wirkt auf Bremse C2 und Kupplung K2)  MHR1 = -57 Nm

•Abtrieb Planetenträger  MPT1 = 243 Nm

•Übersetzung von SRgross zu PT1  iSRgross-PT = 2,693

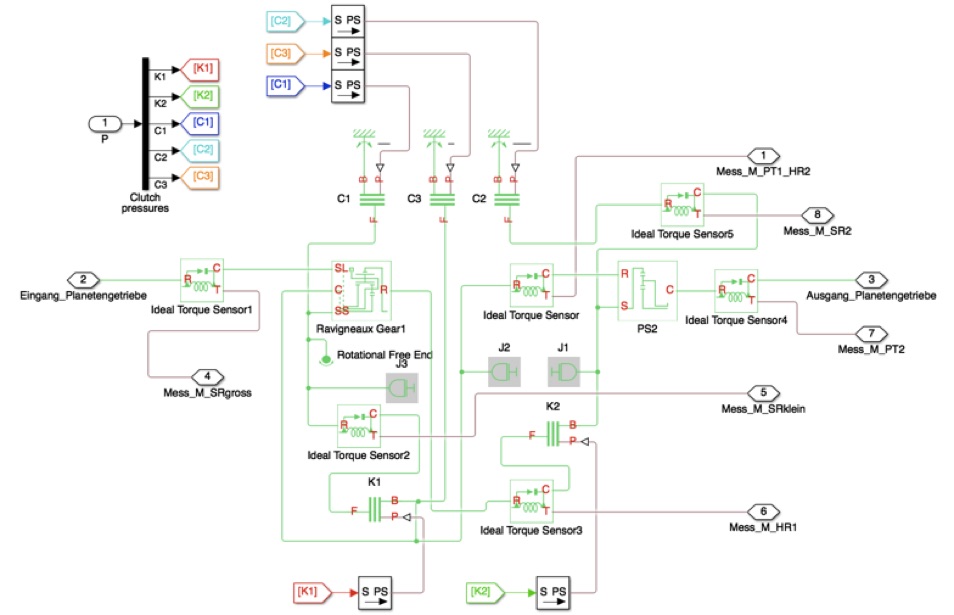
Betrachtung beider Stufen gemeinsam

Im zweiten Schritt schauen wir uns das Gesamt-Getriebe-Modell an. Neben der Ravigneaux-Stufe ist jetzt auch noch die einfache nachgeschaltete Planetenstufe mit ins Modell aufgenommen. Dabei sind die Bremsen und Kupplungen wieder für den ersten Gang fest eingestellt.

Hierbei ist darauf zu achten, dass das komplette Antriebsmoment auch abgerufen wird. Dies kann durch die Gesamtübersetzung und das Reibmoment am Abtrieb eingestellt werden. Bei einer Getriebeübersetzung im ersten Gang von i1G=3,8639 ergibt sich ein Lastmoment größer als 772 Nm, welches über den „Rotational Friction“-Block weggebremst werden muss, um 200 Nm Antriebsmoment auch abzurufen. Wir stellen 900 NM Lastmoment ein. Da der „Ideal Torque Source“-Block nur bis zu 200 Nm erzeugen kann wird dieses voll ausgeschöpft.

Es ergeben sich folgende Drehzahlen und Drehmomente:

Eingang

•SRgross angetrieben mit MSRgross = 200 Nm

•HR1 ist festgebremst  nHR1 = 0 1/min

•Abtrieb SRklein ist freidrehend  MSRklein = 0 Nm

Ausgang

•Momentenbelastung am Planetenträger 1 und am Hohlrad 2  MPT1 = MHR2 = 540 Nm

•Momentenbelastung am Hohlrad 1  MHR1 = -350 Nm

•Momentenbelastung am Planetenträger 2  MPT2 = 770 Nm

•Momentenbelastung am Sonnenrad 2  MSR2 = 570 Nm